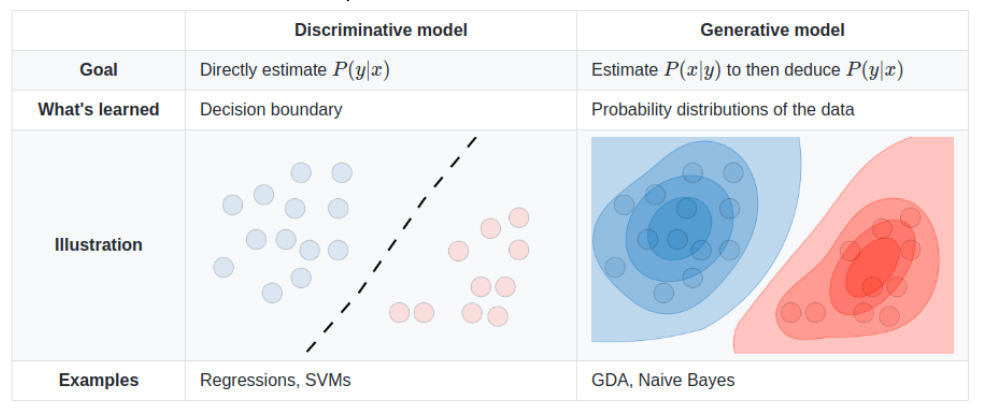
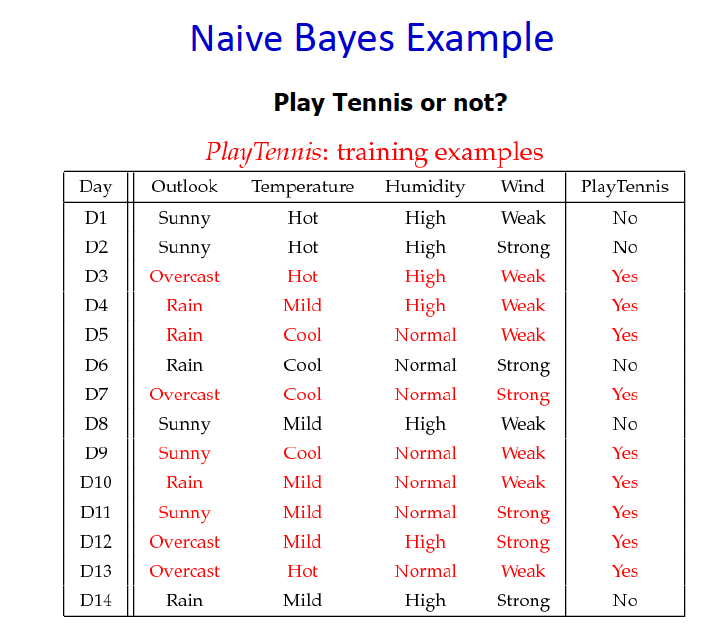
By the end of this article, you would understand how them work. A generative model is actually estimating p(x|y) to then deduce p(y|x).In this case,if we learn the class-conditonal density p(x|Ck) through training, we are able to predict the label for the datapoint x p(Ck|x) = p(x|Ck)p(Ck)/p(x) two models Confused by all the mathematical stuff? Don’t worry, this Naive Bayes example can save your brain cells. example Step one:Sort data cases into bins according to Ck and then compute p(Ck) using frequencies. In this case, we just need to count how many yes and how many no we have. It is obviously that p(yes)=9/14 and p(no)=5/14.

Step two:For each class, estimate p(xi/Ck) for each feature. 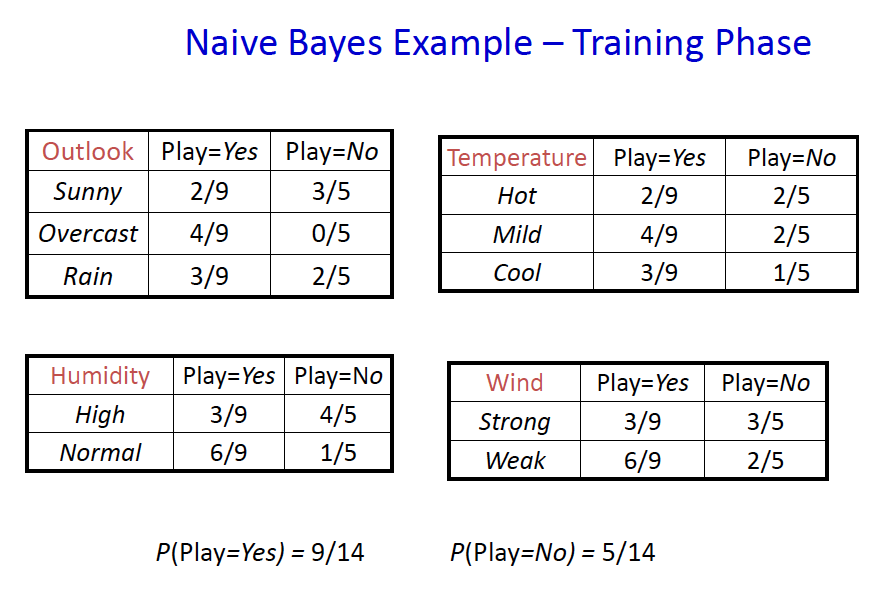example We know that we have 9 yes in variable Outlook and Sunny accounts for 2/9. The rest is also calculate like that.

Step three:Given a new instance, predict its label. example Here, I want to emphsize the calculation is based on the assumption that features are independent.

P(x|Ck)=P(x1,...,xd|Ck)=P(x1|Ck)...P(xd|Ck)

What if we perform Naive Bayes on continuous input like in a Gaussian classifier?

It would have following traits

  • A seperate, diagonal covariance matrix for each class
  • Training is equivalent to fitting a Gaussian to each class.