Whenever we think about model prediction, the first thing pops up is always prediction errors(bisa and variance). Understanding of these errors would help us avoid the mistake of overfitting and underfitting.
WHAT IS BIAS?
Bias is the difference between the average prediction of our model and the the correct value which we are trying to predict.
WHAT IS VARIANCE?
Let me put this way, model with high variance pays a lot of attention to training data and does not generalize on the data which it hasn’t seen before. It performs well on training but has high error on test data.
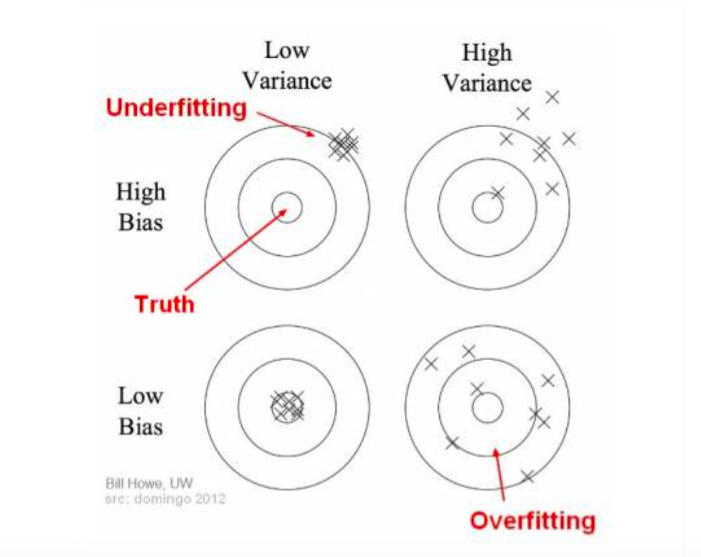
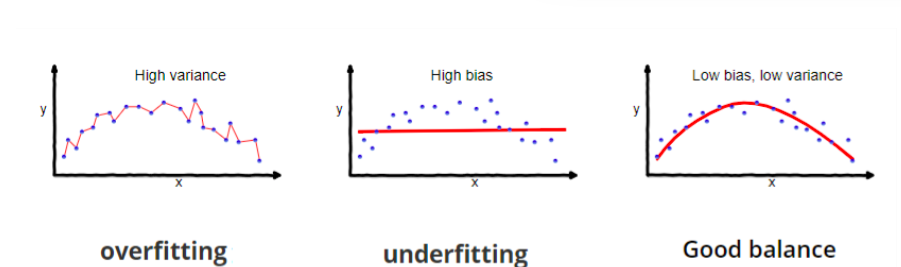
In supervised learning, underfitting means YOUR model messes up the pattern of the data. The prediction is totally wrong! It happens when we have very less amount of data to build an accurate model. Or, we use the wrong method fot data set. In contrast,overfitting happens when our model try to classify every single data point. Usually, these models have low bias and high variance.
TOTAL ERROR
Like always, we need to minimize the error function Total Error = Bias**2 + Variance + Irreducible Error
Here,I want to emphasize the with the increase of algorithem, the bias will go down while the variance goes up. That is why it is important to find a good balance for it.
Now, let us get into the final part—improve your model’s performance. It is basically cross-validation. The main thing is just to repeatedly draw samples from a training set and refit a model of interest on each sample.
CROSS-VALIDATION
cv is used to estimate the test error associated with a model. It simply invovles randomly dividing the dataset into two parts: training set and validation set or hold-out set. We need to keep in mind that only a small subset of the observations are used to fit the model definitely would perform worse.
LEAVE-ONE-OUT CROSS-VALIDATION
It is a better option than the validation set approach cuz we only need one observation for validation and the rest is used to fit the model

K-FOLD CROSS-VALIDATION
This approach invovles randomly dividing the set of observations into k groups of approcimately equal size. The procedure is repeated k times, when a different group is treated as the validation set. It is common to set k equal to 5 or 10.
Whereas LOOCV is computationally intensive for large datasets, k-fold is more general with more accurate estimates of test error.