Why call it a decision tree? This is because you make a bunch of choices until you get to the final decision and the processes are shaped like a tree with all those branches.

How we build a tree?

  • Start at the top of the tree
  • Grow it by splitting features one by one. To determine which feature to split, look at “node impurity”
  • When we get to the bottom, prune the tree to prevent overfitting

Let us talk about CART and then C4.5

Regression trees

Trees are drawn upside down. The final regions are termed leaves. Node is where a split occurs.

To create a regression tree, we use the mean of the response and a greedy approach which focuses on the current step, rather than looking ahead and making a split that will result in a better prediction in a future step.

Classification tree

It is very similar to a regression tree. However, we cannot use the mean value of the response, so we now predict the most commonly occuring class in a region.

I want to use an example to vividly explain how to calculate gini index. GINI(t) = 1 - [p(j|t)]**2

Another algorithm for splitting the tree.

Before we diving into decision tree examples, I need to address Information Theory. For example, a coin flips, we know the prob of being head is 1, we get no imformation from this event. Is that clear.

When we have lots of events, what is the mean information of those events? Assume the events v1,….vj occur with prob p1,p2,….,pj,where[p1,..,pj] is a discrete prob distribution. 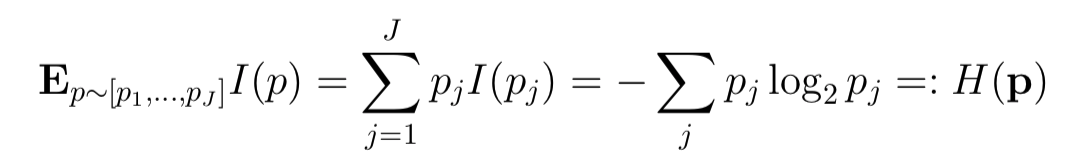information H(p) is called the entropy of discrete distribution p. So if there are only 2 events, with prob = [p,1-p], H(p)=-plog2(p)-(1-p)log2(1-p).

The reason I explained this is that we use infomation gain as the splitting criteria.

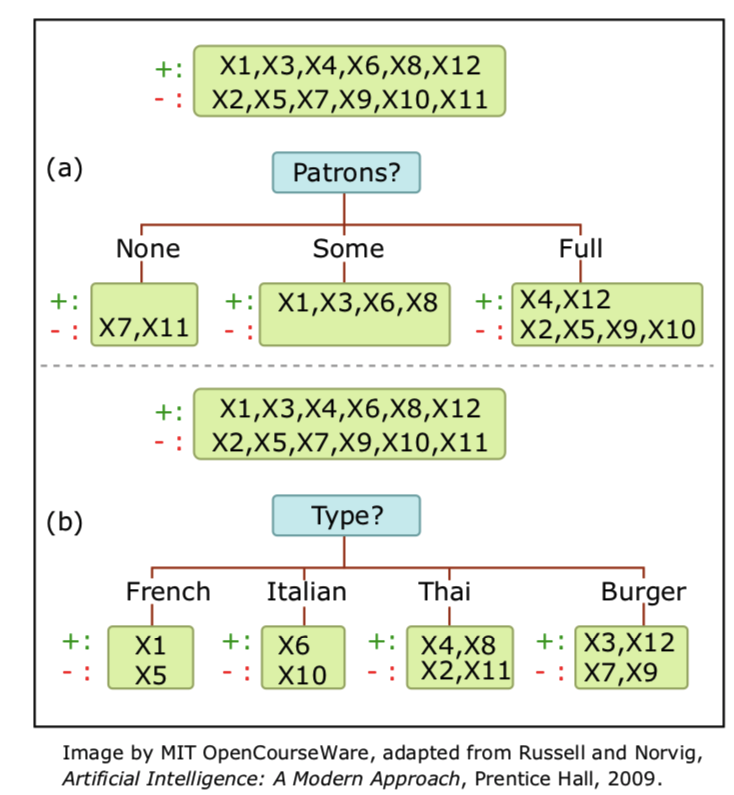
Think about this following example with two options for the first feature. information Gain(S,A) = original entropy - entropy after branching Gain(S,Patrons) = H([0.5,0.5]) - [2/12H[0,1]+4/12H[1,0]+6/12[2/6,4/6]] = 0.541bits Gain(S,Type) = 0bits. In general, we want to choose the feature A that maximize the Gain(S,A).