There are two general strategies to traverse a tree
*Depth First Search(DFS)
In this strategy, we adopt the depth as the priority, so that one can start from the top and reach all the way down to certain left. We can further discuss preorder, inorder, postorder.
*Breadth First Search(BFS)
We scan the tree level by level, following the order of height, from top to bottom. The nodes on higher level woule be visited before the ones in lower level.
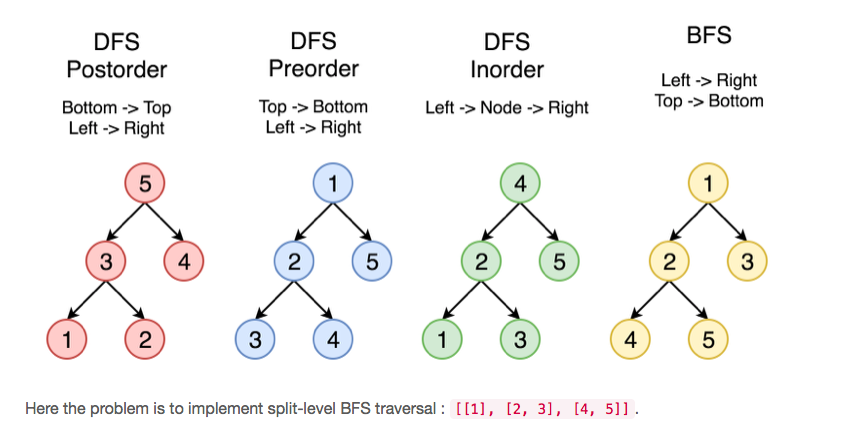
Given a binary tree, return the level order traversal of its nodes’ values. (ie, from left to right, level by level)
Recursion
The output list here is called `levels`, and hence the current level is just a length of this list len(levels). Compare the number of a current level len(levels) with a node level `level`. If you're still on the previous level - add the newone by adding a new list into levels.
Append the node value to the last list in `levels`.
Process recursively child nodes if they are not None : helper(node.left / node.right, level + 1).
We can see from the picture, levels = [], helper(node = 1,level = 0)–>call left helper(node = 2, level = 1)–>right helper(node = 3,level =1),etc–>[[1],[2,3],[4,5]]
class Solution:
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
"""
levels = []
if not root:
return levels
def helper(node, level):
# start the current level
if len(levels) == level:
levels.append([])
# append the current node value
levels[level].append(node.val)
# process child nodes for the next level
if node.left:
helper(node.left, level + 1)
if node.right:
helper(node.right, level + 1)
helper(root, 0)
return levels
Let’s try iteration way to do the BFS.We would keep track of node in queue. In Python the queue implementation with a fast atomic append() and popleft() is deque.
OMG, iteration is so much easier to understand and implement.
We initiate queue with a root and level = 0
While queue is not empty, we add another level to levels, and pop elements from the queue and add the value to the levels. Here we need to keep track of the length of the level to make sure how many times we need to pop!!!
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
from collections import deque
class Solution:
def levelOrder(self, root: TreeNode) -> List[List[int]]:
#this is obiviously a BFS
#push 3 into the queue and length is 1, so we only pop one time
#root has left and right, level_length is 2, so we pop [9,20] to current
#[[3],[9,20]...]
levels = []
if not root:
return levels
level = 0
queue = deque([root,])
while queue:
level_length = len(queue)
levels.append([])#current layer
for i in range(level_length):
node = queue.popleft()
levels[level].append(node.val)
#add next layer element into queue
if node.left:
queue.append(node.left)
if node.right:
queue.append(node.right)
#go to next level
level += 1
return levels
let us do some inorder traveral with iteration, usually it is DFS and we gonna use stack this time. Take a deep breath and you can do it.
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
#use stack to dig into the bottom and start to check the right
res = []
stack = []
curr = root
while (curr is not None or len(stack) > 0):
while curr is not None:#if right is not None,add right and check left
stack.append(curr)
curr = curr.left
node = stack.pop()
res.append(node.val)
#this is used to check the right when we hit the bottom
curr = node.right
return res
Validate Binary Search Tree
We need to keep in mind that root value is bigger than its left and smaller thanits right. Attention: root.val is the maximum of the left_subtree.
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# cuz we r comparing the value in tree, so we do a in-order traverse, which is
# preorder DFS, so root->left->right from top to bottom, sorta similar to BFS
class Solution:
def isValidBST(self, root: TreeNode) -> bool:
if not root:
return True
stack = [(root,float('-inf'),float('inf'))]
# use set for remove duplicated value
while stack:
node,_min,_max = stack.pop()
if node.val <= _min or node.val >= _max: return False
if node.left:
#here, we want root.left value compared with its root value
stack.append((node.left,_min,min(_max,node.val)))
if node.right:
stack.append((node.right,max(_min,node.val),_max))
return True